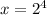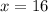Answer:
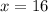
Explanation:
Given
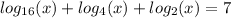
Required
Solve for x
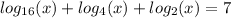
Change base of 16 and base of 4 to base 2
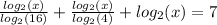
Express 16 and 4 as 2^4 and 2^2 respectively
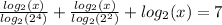
The above can be rewritten as:
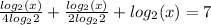
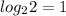
So, we have:
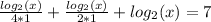
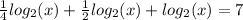
Multiply through by 4
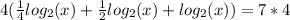
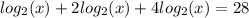
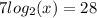
Divide through by 7
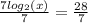
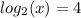
Apply the following law of logarithm:
If
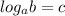 Then
Then
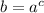
So, we have: