Question

Solve by using elimination. Express your answer as an ordered pair.

Answer 1

(3, 5)

Step-by-step explanation:

Since none of the x y coeficcints are the same, we need to multiply entire equations

3(2x+5y=31)=6x+15y=93

2(3x-2y=-1)=6x-4y=-2

Now we have the same x coeficcionts!

(6x+15y=93)-(6x-4y=-2)=19y=95

we then divide 19 on both sides to get:

y=5

Now we know what y is, we'll need to plug 5 in for y in the second equation.

3x-2(5)=-1

3x-10=-1

3x=9

x=3

Answer 2

Greetings again.

The answer is (3,5)

Step-by-step explanation:

Other previous questions about the System of Two Variables Linear Equations. Previous questions, both y-terms have the same absolute-values but different operator/sign. Some questions previously have same operators as we multiply one of the equation by -1 to eliminate.

But this question, there are no terms that are same. Especially not the same looking value.

And what do we do if it's like this?

The answer is, do something to make both equations have same absolute value but different operators.

That is to multiply. For this question, I'll be eliminating x-term. So I'll multiply both equations to make the x-term have same absolute-value and different operator.

Because 2 and 3 can multiply into 6. Therefore, multiply the whole first equation by 3 and multiply the whole second equation by 2.

`\left \{ {{2x+5y=31} \atop {3x-2y=-1}} \right. \\\left \{ {{2x(3)+5y(3)=31(3)} \atop {3x(2)-2y(2)=-1(2)}} \right. \\\left \{ {{6x+15y=93} \atop {6x-4y=-2}} \right.`

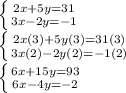
This is our new equations. Since we need to eliminate x-term. We multiply one of the equation by -1. I'll choose the second equation to multiply.

`6x(-1)-4y(-1)=-2(-1)\\-6x+4y=2`

`\left \{ {{6x+15y=93} \atop {-6x+4y=2}} \right.`

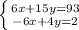
Then proceed with add/subtract vertically

6x-6x = 0

15y+4y = 19y

93+2 = 95

Therefore, we get 19y = 95

`19y=95\\y=(95)/(19) \\y=5`

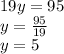
Our y-value is 5. However, we are not done yet. Since this is the System of Two Variables Linear Equation. We need to find the x-value too to express in ordered pairs. (x,y)

Choose any given equations to substitute y = 5 in. I'll substitute y = 5 in 3x-2y=-1

`3x-2y=-1`

Substitute y = 5 in the equation.

`3x-2(5)=-1\\3x-10=-1\\3x=-1+10\\3x=9\\x=3`

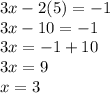
Thus, when y = 5, x = 3 or when x = 3, y = 5. As the ordered pairs = (x,y) Therefore, the answer is (3,5)