Question

A box is sitting stationary on a long level ramp on level ground. The coefficient of static friction is (1.0). One end of the ramp is slowly lifted higher and higher. What is the angle of the ramp with respect to the ground when the box begins slidig?

Answer 1

45 degrees

Step-by-step explanation:

Given that the coefficient of friction,
`\mu=1.0`

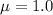
Let the angle of the ramp be
`\theta`.

The gravitational force acting downward
`=mg`

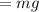
The normal reaction by the ramp on the box,
`N=mg\cos\theta`

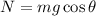
So, the maximum frictional force that can act on the box,
`f= \mu N`

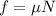
The force along with the plane in the direction of sliding,
`F = mg\sin\theta`

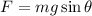
When the box begins sliding, the F must have to overcome the frictional force,f.

So, F=f

`mg\sin\theta=\mu N \\\\mg\sin\theta=\mu mg\cos\theta \\\\\frac {\sin\theta}{\cos\theta}=\mu \\\\\tan\theta=\mu \\\\\theta=\tan^(-1)\mu \\\\`

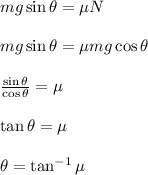
Putting the value of \mu, we have

`\theta=\tan^(-1)1`

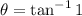
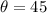`\theta=45` degrees.

Hence, the angle of the ramp with respect to the ground when the box begins sliding is 45 degrees.