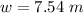Question

The opening to a cave is a tall, 30.0-cm-wide crack. A bat is preparing to leave the cave emits a 30.0 kHz ultrasonic chirp. How wide is the "sound beam" 100. M outside the cave opening? Use v sound= 340. M/s.

Answer 1

The value is
`w = 7.54 \ m`

Step-by-step explanation:

From the question we are told that

The length of the crack is
`a = 0.3 \ m`

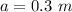
The frequency is
`f = 30.0 \ kHz = 30 *10^(3) \ Hz`

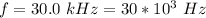
The distance outside the cave that is being consider is
`D = 100 \ m`

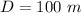
The speed of sound is
`v_s = 340 \ m/s`

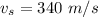
Generally the wavelength of the wave is mathematically represented as

`\lambda = \frac{v}f}`

=>
`\lambda = (340 )/(30*10^(3))`

=>
`\lambda = 0.0113 \ m/s`

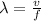
Generally for a single slit the path difference between the interference patterns of the sound wave and the center is mathematically represented as

`y = ( n * \lambda * D)/(a)`

=>
`y = ( 1 * 0.0113 * 100)/(0.3)`

=>
`y = 3.77 \ m`

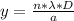
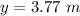
Generally the width of the sound beam is mathematically represented as

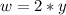
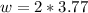
`w = 2 * y`

=>
`w = 2 * 3.77`

=>
`w = 7.54 \ m`