Question

Solve by using elimination. Express your answer as an ordered pair.

Answer 1

Greetings again.

The answer is (-3,6)

Step-by-step explanation:

As explained in the your previous question about eliminating the term.

We can either eliminate x-term or y-term to find/solve another term first. But It's easier to eliminate the term without multiplying to make both terms the same.

By adding/subtracting vertically for two equations. We get that the adding y and -y makes them 0.

Therefore, we eliminate y-term to solve x first.

`\left \{ {{2x+y=0} \atop {3x-y=-15}} \right. \\5x=-15\\`

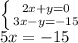
I explained about adding/subtracting vertically.

Basically, 2x+3x = 5x

y - y = 0

0 - 15 = -15

That's how to get 5x = -15

`x=-3`

Because it is the system of two linear equations. We need to find the y-term too.

Therefore, substitute x = -3 in any given equations. I suggest you to substitute x = -3 in the equation with less coefficient value.

So I'll substitute x = -3 in 2x+y = 0 instead because the first equation has less coefficient than the second equation.

`2x+y=0`

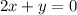
Substitute x = -3 in the equation.

`2(-3)+y=0\\-6+y=0\\y=6`

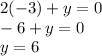
Therefore, when x = -3, y = 6. Since you want the answer as an ordered pair. The answer is (-3,6)