Question

If |x-1| = |x+5|, find the value of x.

Answer 1

Greetings.

The answer is x = -2.

Step-by-step explanation:

By solving the Absolute-Value Equation. We give them 2 conditions.

When x ≥ 0 and When x < 0

The different is that When x ≥ 0, |x-a| = x-a as defined.

And when x < 0. |x-a| = -x+a as defined.

( 1 ) - When x ≥ 0 for |x-1| and |x+5|

When x ≥ 0, |x-1| = x-1 and |x+5| = x+5

Therefore, x-1 = x+5

`x-1=x+5\\x-x=5+1\\0=6`

Because the equation is false. Therefore, The condition (1) doesn't apply.

( 2 ) - When x ≥ 0 for |x-1| and x < 0 for |x+5|

This time, we try another condition.

When x ≥ 0, |x-1| = x-1 and When x < 0, |x+5| = -x-5.

`x-1=-x-5\\x+x=-5+1\\2x=-4\\x=-(4)/(2)\\x=-2`

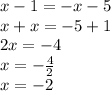
And we get the answer, |x-1| = |x+5| when x = -2.

But we haven't tried the last condition.

( 3 ) And that is when x < 0 for both terms.

|x-1| = -x+1 (x < 0)

|x+5| = -x-5 (x < 0)

`-x+1=-x-5\\-x+x=-5-1\\0=-6`

The equation is not true. Therefore, the answer is x = -2.