Answer:
(a) The area of the triangle is approximately 39.0223 cm²
(b) ∠SQR is approximately 55.582°
Explanation:
(a) By sin rule, we have;
SQ/(sin(∠SPQ)) = PQ/(sin(∠PSQ)), which gives;
5.4/(sin(52°)) = 6.8/(sin(∠PSQ))
∴ (sin(∠PSQ)) = (6.8/5.4) × (sin(52°)) ≈ 0.9923
∠PSQ = sin⁻¹(0.9923) ≈ 82.88976°
Similarly, we have;
5.4/(sin(52°)) = SP/(sin(180 - 52 - 82.88976))
Where, 180 - 52 - 82.88976 = ∠PQS = 45.11024
SP = 5.4/(sin(52°))×(sin(180 - 52 - 82.88976)) ≈ 4.8549
Given that RS : SP = 2 : 1, we have;
RS = 2 × SP = 2 × 4.8549 ≈ 9.7098
We have by cosine rule,
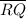 ² =
² =
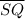 ² +
² +
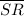 ² - 2 ×
² - 2 ×
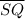 ×
×
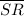 × cos(∠QSR)
× cos(∠QSR)
∠QSR and ∠PSQ are supplementary angles, therefore;
∠QSR = 180° - ∠PSQ = 180° - 82.88976° = 97.11024°
∠QSR = 97.11024°
Therefore;
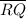 ² = 5.4² + 9.7098² - 2 × 5.4×9.7098× cos(97.11024)
² = 5.4² + 9.7098² - 2 × 5.4×9.7098× cos(97.11024)
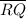 ² ≈ 136.42
² ≈ 136.42
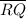 = √(136.42) ≈ 11.6799
= √(136.42) ≈ 11.6799
The area of the triangle = 1/2 ×
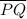 ×
×
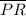 × sin(∠SPQ)
× sin(∠SPQ)
By substituting the values, we have;
1/2 ×
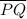 ×
×
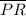 × sin(∠SPQ)
× sin(∠SPQ)
1/2 × 6.8 × (4.8549 + 9.7098) × sin(52°) ≈ 39.0223 cm²
The area of the triangle ≈ 39.0223 cm²
(b) By sin rule, we have;
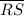 /(sin(∠SQR)) =
/(sin(∠SQR)) =
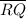 /(sin(∠QSR))
/(sin(∠QSR))
By substituting, we have;
9.7098/(sin(∠SQR)) = 11.6799/(sin(97.11024))
sin(∠SQR) = 9.7098/(11.6799/(sin(97.11024))) ≈ 0.82493
∠SQR = sin⁻¹(0.82493) ≈ 55.582°.