Substituting x with π/2 - x gives the equivalent integral,
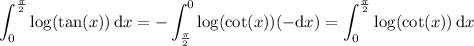
So if we let J denote the value of the integral, we have
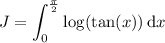
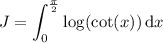
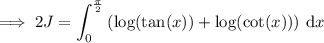
Condensing the logarithms, we have
log(tan(x)) + log(cot(x)) = log(tan(x) cot(x)) = log(1) = 0
since cot(x) = 1/tan(x), which means
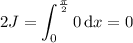
and so the original integral has a value of J = 0.