Question

Find the 75th term of the following arithmetic sequence 16,25,34,43

Answer 1

`\boxed {\boxed {\sf 682}}`

Explanation:

The nth term of an arithmetic sequence can be found using the following formula.

`a_n=a+d(n-1)`

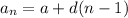
where a is the first term, d is the common difference, and n is the term.

First, we should find the common difference.

We can do this by subtracting each term from the term following it. Basically, subtract the first term from the second term, the second from the third, and so on.

`d= a_2-a_1`

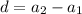
The second term is 25 and the first is 16.

`d= 25-16`

`d=9`

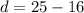
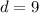
Now we know the common difference is 9. We also know the first term is 16 and we are looking for the 75th term.

`d=9 \\a=16 \\n= 75`

Substitute the values into the formula.

`a_(75)=16+9(75-1)`

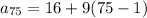
Solve according the PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction).

Solve the parentheses first.

`a_(75)=16+9(74)`

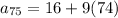
Multiply next.

`a_(75)=16+666`

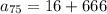
Finally, add.

`a_(75)=682`

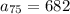
The 75th term in the sequence is 682.