Answer:
Approximately 11 feet.
Explanation:
Let the length of the third side of the triangle be represented by x. Applying Cosine rule, we have:
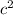 =
=
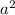 +
+
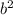 - 2abCos C
- 2abCos C
⇒
 =
=
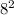 +
+
 - 2(8 x 12) Cos
- 2(8 x 12) Cos
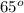
= 64 + 144 - 192 x 0.42262
= 208 - 81.143
= 126.857
x =
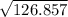
= 11.2631
x ≅ 11
The length of the third side of the triangle is approximately 11 feet.