Question

Which inequality correctly compares Three-fourths, One-seventh, and Five-sixths? One-seventh < Three-fourths < Five-sixths One-seventh < Five-sixths < Three-fourths Three-fourths < Five-sixths < One-seventh Three-fourths < One-seventh < Five-sixths

Answer 1

d

Explanation:

Answer 2

The inequality which correctly compares Three-fourths, One-seventh, and Five-sixths is : One-seventh < Three-fourths < Five-sixths.

The first option is correct.

Explanation:

To determine which inequality correctly compares Three-fourths, One-seventh, and Five-sixths, we will arrange them in ascending order.

To do this, first, we will determine the LCM of the fractions denominators..

Three-fourths, One-seventh, and Five-sixths

`(3)/(4), (1)/(7), and (5)/(6)`

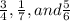
The denominators are 4, 7 and 6.

LCM of 4,7 and 6 is 84

Then, we will write the fractions in a form whereby they all have the same denominators.

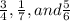`(3)/(4), (1)/(7), and (5)/(6)` can be written as

`(63)/(84), (12)/(84), and (70)/(84)`

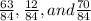
The resulting order of the numerators gives the order of the fractions.

Now, we will arrange
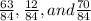`(63)/(84), (12)/(84), and (70)/(84)` in ascending order. This becomes

`(12)/(84), (63)/(84),and (70)/(84)`.

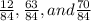∴ The ascending order of the fractions is
`(1)/(7), (3)/(4),and (5)/(6)`.

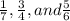That is, One-seventh, Three-fourths, and Five-sixths.

Hence, we can write that

One-seventh < Three-fourths < Five-sixths.

This is the inequality which correctly compares Three-fourths, One-seventh, and Five-sixths