Answer:
The width of the carpet is 12 inches and the length of the carpet is 120 inches.
Explanation:
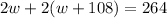
^We can distribute first^
Distributing would result in:
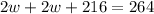
Then we would combine like terms, which would result in:
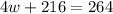
Then we solve the equation.
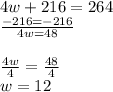
Since the width of the carpet is 12 (as we figured out). The statement said that "The length of the carpet is 108 inches more than the width."
So now we add 108 to 12 to figure out the length.
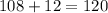
The length of the carpet is 120 inches.