Question

Write a rational function with an x-intercept at (-9,0), a vertical asymptote at x=3, and a hole located at (1,-5). Then, identify the horizontal asymptote.

Answer 1

The rational function is
`f(x) = (x^2 + 8\cdot x - 9)/(x^2 - 4 \cdot x + 3)`

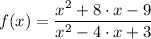
The horizontal asymptote occur at y = 1

Explanation:

Given that the function has an x-intercept at (-9, 0), we have;

(x + 9) is a factor of the function

Also, given that the function has a vertical asymptote at x = 3, we have that a factor of the denominator of the function is (x - 3)

With a hole at (1, -5), we have, (x - 1) in both the numerator and the denominator and when x = 1, f(x) = -5

The general form of the function can be presented as follows;

f(x) = ((x + 9)·(x - 1))/((x - 3)(x - 1)) = (x² + 8·x - 9)/(x² - 4·x + 3)

Given that the power of the numerator and the denominator are equal, the horizontal asymptote occur at ratio of the leading coefficient of the numerator and the denominator which from the above equation is 1/1 = 1

The horizontal asymptote occur at y = 1

Please find attached the graph of the function created with Microsoft Excel