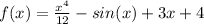Answer:
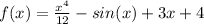
General Formulas and Concepts:
Calculus
- Antiderivatives
- Integration Constant C
- [Int Rule] Reverse Power Rule:
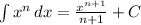
- Integration Property 1:
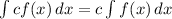
- Integration Property 2:
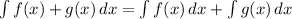
Explanation:
Step 1: Define
f"(x) = x² + sin(x)
Condition f'(0) = 2
Condition f(0) = 4
Step 2: Integrate Pt. 1
- Set up:
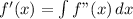
- Substitute:
![f'(x) = \int [{x^2 + sin(x)}] \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/xr4s8z8a968ncupe6etp08kx5k67njzhqh.png)
- Rewrite [Int Property 2]:
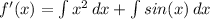
- Integrate [Reverse Power Rule/Trig]:
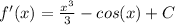
Step 3: Find f'(x)
Use the given condition to find the differential equation.
- Substitute:
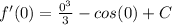
- Substitute:
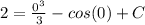
- Evaluate:
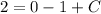
- Solve:
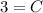
- Define:
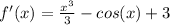
Step 4: Integrate Pt. 2
- Set up:
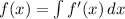
- Substitute:
![f(x) = \int [{(x^3)/(3) - cos(x) + 3}] \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/85npxjrl01zzj8qg3k8hcchli006dtlxbi.png)
- Rewrite [Int Property 2]:
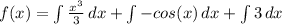
- Rewrite [Int Property 1]:
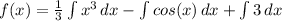
- Integrate {Reverse Power Rule/Trig]:
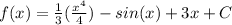
- Simplify:
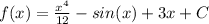
Step 5: Find f(x)
Use the given condition to find the equation.
- Substitute:
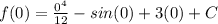
- Substitute:
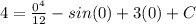
- Evaluate:
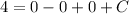
- Solve:
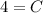
- Define: