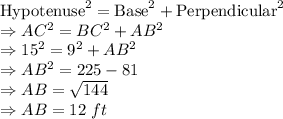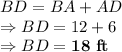Question

Please help fast its really important ;-; The base of a 15 foot ladder is 9 feet from a building. The top of the leaning ladder reaches and makes contact with the building's roof. On the corner of the building, a 6 foot flagpole is erected on the roof. What is the height from the base of the building to the top of the flagpole?

Answer 1

18 ft

Explanation:

Given that:

Length of ladder = 15 ft

Distance of ladder's foot from the building = 9 ft

Height of flagpole erected on the roof = 6 ft

To find:

Height of the top of flagpole from the base of the building?

Solution:

The given situation can be represented from the figure as attached in the answer area.

We have to find the length of
`BD`.

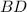There is a right angle
`\triangle ABC`, right angled at point
`B\\`.

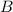We can use Pythagorean theorem here to find the side
`BA`.

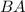As per Pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow AC^(2) = BC^(2) + AB^(2)\\\Rightarrow 15^2 = 9^2+AB^2\\\Rightarrow AB^2 = 225-81\\\Rightarrow AB = \sqrt {144}\\\Rightarrow AB =12\ ft`

`BD = BA + AD\\\Rightarrow BD = 12 + 6\\\Rightarrow BD = \bold{18\ ft}`