Answer:
The eccentricity of the ellipse is 0.252.
Step-by-step explanation:
The eccentricity of an ellipse (
 ), dimensionless, can be determined by means of the following expression:
), dimensionless, can be determined by means of the following expression:
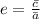 (1)
(1)
Where:
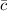 - Distance between the foci, dimensionless.
- Distance between the foci, dimensionless.
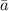 - Length of the major axis, dimensionless.
- Length of the major axis, dimensionless.
If we know that
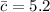 and
and
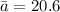 , then the eccentricity of the ellipse is:
, then the eccentricity of the ellipse is:
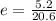
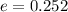
The eccentricity of the ellipse is 0.252.