Answer:
It will take 43.37 mins for the cake to cook off to 90
Explanation:
From Newton's law of cooling

Where
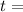 time
time
 = Temperature of the given body at time
= Temperature of the given body at time
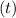
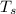 = Surrounding temperature
= Surrounding temperature
 = Initial temperature of the body
= Initial temperature of the body
and
 = constant
= constant
From the question,
 = 357
= 357
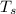 = 72
= 72
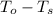 = 357 - 72 = 285
= 357 - 72 = 285
∴
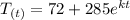
From the question, the cake cools to 130 after 25 min. Then, we can write that
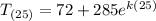
∴
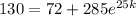
Then,
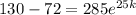
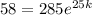
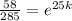
Take the natural log (ln) of both sides
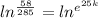
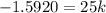
∴
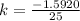

Now, to determine how long it take for the cake to cook off to 90
That is,
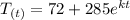
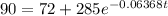
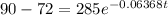
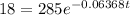

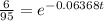
Take the natural log (ln) of both sides
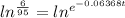
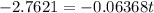
∴
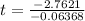
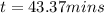
Hence, it will take 43.37 mins for the cake to cook off to 90.