Question

If $300 is invested at a rate of 5% per year and is compounded quarterly, how much will the investment be worth in 15 years?

Use the compound interest formula A equals P times the quantity 1 plus r divided by n end quantity raised to the power of n times t.

$141.04
$361.45
$515.28
$632.15

Answer 1

$632.15

Explanation:

I got it right on the test.

Answer 2

$632.15

Explanation:

Compound Interest Formula

`\large \text{$ \sf A=P\left(1+(r)/(n)\right)^(nt) $}`

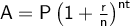
where:

• A = final amount
• P = principal amount
• r = interest rate (in decimal form)
• n = number of times interest applied per time period
• t = number of time periods elapsed

Given:

• P = $300
• r = 5% = 0.05
• n = 4 (quarterly)
• t = 15 years

Substitute the given values into the formula and solve for A:

`\implies \sf A=300\left(1+(0.05)/(4)\right)^(4 * 15)`

`\implies \sf A=300\left(1.0125}\right)^(60)`

`\implies \sf A=632.1544041`

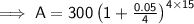
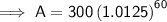
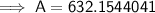
Therefore, the investment will be worth $632.15 in 15 years.