Question

A plane at an altitude of 7000ft is flying in direction of an island. If they angel of depression is 21 from the plane to the island, what is the horizontal distance until the plane flies over the island?

Answer 1

The horizontal distance until the plane flies over the island is 2687ft

Explanation:

An illustrative diagram of the scenario is shown in the attachment below.

P is the position of the plane, I indicates the position of the island and G is point on the ground such that /PG/ is perpendicular to the ground.

From the diagram, the horizontal distance from the plane to the island is x.

x = /IG/

In the diagram, consider triangle PIG which is a right angle triangle.

/PI/ is the hypotenuse

/IG/ is the opposite

and /GP/ is the adjacent.

From the formula,

`tan\theta = (opposite)/(adjacent)\\`

∴
`tan\theta = (/IG/)/(/GP/)\\`

`tan\theta = (x)/(/GP/)\\`

∴
`x = /GP/ tan\theta`

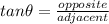
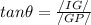
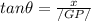
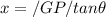
From the diagram

/GP/ = 7000 ft and
`\theta = 21`

∴
`x = 7000 * tan21\\`

`x = 2687.05 ft`

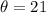
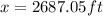
`x` ≅ 2687 ft

Hence, the horizontal distance until the plane flies over the island is 2687ft