Question

A ball is thrown vertically upward with an initial velocity of 96 feet per second. the distances (in feet) of the ball from the ground after t seconds is s(t)=96t-16t^2.

a.) At what time t will the ball strikes the ground?
b.) from what time t is the ball more than 138ft above the ground?​

Answer 1

a) The ball strikes the ground at 6 seconds

b) The ball will be at more than 138 ft above the ground when the time is between 2.39 s and 3.61 s

Explanation:

The distance of the ball from the ground after t seconds is modeled by the equation:

`s(t)=96t-16t^2`

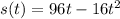
a) The ball is at ground level when s=0, thus:

`96t-16t^2=0`

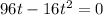
Factoring:

`t(96-16t)=0`

There are two solutions:

t=0

96-16t=0

The first solution corresponds to the moment when the ball is thrown upward.

The second solution comes from:

96-16t=0

Solving:

t = 96/16 = 6 s

The ball strikes the ground at 6 seconds.

b)The ball will have a distance of more than 138 ft above the ground when:

`96t-16t^2>138`

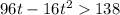
Rearranging:

`16t^2-96t+138<0`

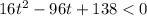
Factoring:

`(t-3.61)(t-2.39)<0`

This inequality is satisfied when t lies in the interval:

(2.39,3.61)

The ball will be at more than 138 ft above the ground when the time is between 2.39 s and 3.61 s