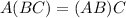Question

Prove that A(BC)=(AB)C as the associative law of matrix multiplication​

Answer 1

`A\left(BC\right)=\begin{pmatrix}7&13\\ \:15&29\end{pmatrix}`

`\left(AB\right)C=\begin{pmatrix}7&13\\ \:15&29\end{pmatrix}`

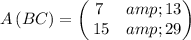
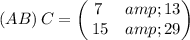
Therefore, we conclude that

`A(BC)=(AB)C`

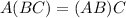
Explanation:

Given that the associative law of matrix multiplication​

`A(BC)=(AB)C`

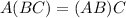
Let

`A=\begin{pmatrix}1&2\\ 3&4\end{pmatrix}`

`B\:=\:\begin{pmatrix}1&0\\ 1&2\end{pmatrix}`

`C=\begin{pmatrix}1&3\\ \:1&1\end{pmatrix}`

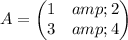
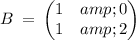
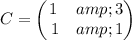
proving

A(BC)=(AB)C

Determining the L.H.S

• A(BC)

`A\left(BC\right)=\begin{pmatrix}1&2\\ \:\:3&4\end{pmatrix}\:\left[\:\begin{pmatrix}1&0\\ \:\:\:1&2\end{pmatrix}\begin{pmatrix}1&3\\ \:\:\:\:1&1\end{pmatrix}\right]\:`

First determining BC

as multiplying the rows of the first matrix by the column of the second matrix

`BC=\begin{pmatrix}1&0\\ \:1&2\end{pmatrix}\begin{pmatrix}1&3\\ \:1&1\end{pmatrix}=\begin{pmatrix}1\cdot \:\:1+0\cdot \:\:1&1\cdot \:\:3+0\cdot \:\:1\\ \:1\cdot \:\:1+2\cdot \:\:1&1\cdot \:\:3+2\cdot \:\:1\end{pmatrix}`

`=\begin{pmatrix}1&3\\ 3&5\end{pmatrix}`

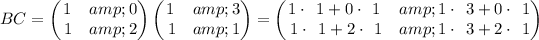
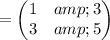
so the matrix equation becomes

`A\left(BC\right)=\begin{pmatrix}1&2\\ \:\:3&4\end{pmatrix}\begin{pmatrix}1&3\\ \:3&5\end{pmatrix}`

`=\begin{pmatrix}1\cdot \:1+2\cdot \:3&1\cdot \:3+2\cdot \:5\\ 3\cdot \:1+4\cdot \:3&3\cdot \:3+4\cdot \:5\end{pmatrix}`

`=\begin{pmatrix}7&13\\ 15&29\end{pmatrix}`

`A\left(BC\right)=\begin{pmatrix}7&13\\ \:15&29\end{pmatrix}`

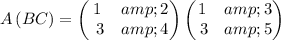
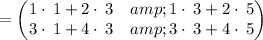
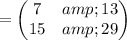
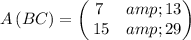
Determining the R.H.S

• (AB)C

`\left(AB\right)C=\left[\begin{pmatrix}1&2\\ \:\:\:\:3&4\end{pmatrix}\:\begin{pmatrix}1&0\\ \:1&2\end{pmatrix}\right]\begin{pmatrix}1&3\\ \:\:\:\:\:1&1\end{pmatrix}\:`

First determining AB

as multiplying the rows of the first matrix by the column of the second matrix

`AB=\begin{pmatrix}1&2\\ \:\:3&4\end{pmatrix}\begin{pmatrix}1&0\\ \:\:1&2\end{pmatrix}=\begin{pmatrix}1\cdot \:\:1+2\cdot \:\:1&1\cdot \:\:0+2\cdot \:\:2\\ \:3\cdot \:\:1+4\cdot \:\:1&3\cdot \:\:0+4\cdot \:\:2\end{pmatrix}`

`=\begin{pmatrix}3&4\\ 7&8\end{pmatrix}`

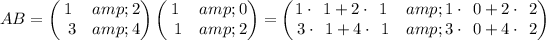
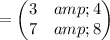
so the matrix equation becomes

`AB\left(C\right)=\begin{pmatrix}3&4\\ \:\:7&8\end{pmatrix}\begin{pmatrix}1&3\\ \:\:1&1\end{pmatrix}`

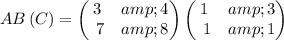
multiplying the rows of the first matrix by the column of the second matrix

`=\begin{pmatrix}3\cdot \:1+4\cdot \:1&3\cdot \:3+4\cdot \:1\\ 7\cdot \:1+8\cdot \:1&7\cdot \:3+8\cdot \:1\end{pmatrix}`

`=\begin{pmatrix}7&13\\ 15&29\end{pmatrix}`

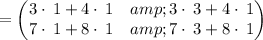
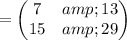
Thus,

`\left(AB\right)C=\begin{pmatrix}7&13\\ \:15&29\end{pmatrix}`

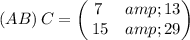
as

`A\left(BC\right)=\begin{pmatrix}7&13\\ \:15&29\end{pmatrix}`

`\left(AB\right)C=\begin{pmatrix}7&13\\ \:15&29\end{pmatrix}`

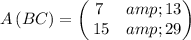
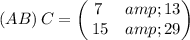
Therefore, we conclude that

`A(BC)=(AB)C`