Question

A particle moves along the x-axis so that its position at time 1 > 0 is given by x(t) and dx/dt = -10t⁴+9t² + 8t. The acceleration of the particle is zero when t=

a. 0.387
b. 0.831
c. 1.243
d. 1.647
e. 8.094​

Answer 1

Given:

A particle moves along the x-axis so that its position at time t > 0 is given by x(t).

`(dx)/(dt)=-10t^4+9t^2+8t`

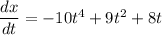
To find:

The value of t at which acceleration of the particle is zero.

Solution:

We have, x(t) as position function. So, its derivative with respect to t is velocity.

`v=(dx)/(dt)=-10t^4+9t^2+8t`

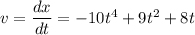
Derivative of velocity with respect to t is acceleration.

`a=(dv)/(dt)=(d)/(dt)(-10t^4+9t^2+8t)`

`a=-10(4t^3)+9(2t)+8(1)`

`a=-40t^3+18t+8`

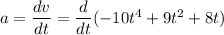
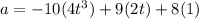
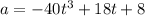
Putting a=0, to find the time t at which acceleration of the particle is zero.

`0=-40t^3+18t+8`

`0=-40t^3+18t+8`

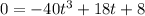
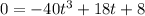
Using the graphing calculator, we get t=0.831 is the only real solution of this equation.

`t=0.831`

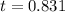
Therefore, the correct option is b.