-------------------------------------------------------------------------------------------------------------
Answer:
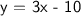
-------------------------------------------------------------------------------------------------------------
Given:
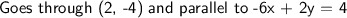
Find:
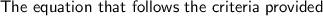
Solution: First we need to solve for y in the equation that was provided so we can get the slope. Then we plug in the values into the point-slope formula and then solve for y to get our final equation.
Add 6x to both sides
Divide both sides by 2
Plug in the values
Distribute and simplify
Subtract 4 from both sides
Therefore, the equation that follows the information that was provided in the problem statement is y = 3x - 10.