Question

Find the x-value for point C such that AC and BC from a 2:3 ratio.

Answer 1

Given:

Point C divides AB such that AC:BC=2:3.

To find:

The x-value for point C.

Solution:

Section formula: If a point divide a line segment in m:n, then

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

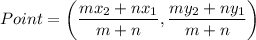
Form the given graph it is clear that the endpoints of the line segment AB are A(-3,5) and B(3,0).

Point C divides AB such that AC:BC=2:3. Using section formula, the coordinates of point C are

`C=\left((2(3)+3(-3))/(2+3),(2(0)+3(5))/(2+3)\right)`

`C=\left((6-9)/(5),(0+15)/(5)\right)`

`C=\left((-3)/(5),(15)/(5)\right)`

`C=\left(-0.6,3\right)`

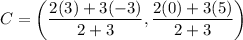
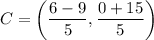
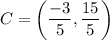
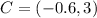
The x-value of C is -0.6.

Therefore, the correct option is B.