Answer:
Explanation:
G is the incenter of ΔABC,
Incenter of a triangle is defined by the point where angle bisectors of the interior angles intersect.
10). m∠ABG = m∠CBG = 25°
11). m∠BCG = m∠ACG = 18°
Therefore, m∠BCA = m∠BCG + m∠ACG = 2×18° = 36°
12). m∠ABC + m∠BAC + m∠ACB = 180°
2(25)° + m∠BAC + 36° = 180°
m∠BAC = 180° - 86° = 94°
13). m∠BAG =
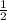 (m∠BAC) = 47°
(m∠BAC) = 47°
14). Since, incenter is equidistant from all sides of the triangle,
Therefore, DG = GF = FE = 4 units
15). In right triangle BEG,
tan(25)° =
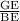
BE =
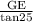
=
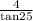
BE = 8.6
16). In right triangle BEG,
cos(25)° =
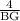
BG =
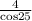 = 4.4
= 4.4
17). In right triangle GEC,
sin(18)° =
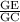
GC =
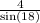 = 12.9
= 12.9