Question

When 7/11 is written as a decimal, what is the sum of the first 20 digits after the decimal point? Pls Help

Answer 1

90

Explanation:

Using long division, we find that Every group of two digits after the decimal point has a sum of 9 so the sum of the first 20 digits after the decimal point is 10*9=90

Answer 2

There's a neat trick to finding the rational form of a repeating decimal number. Take for instance
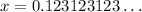`x=0.123123123\ldots`. Then

`x = 0.123123123\ldots \\\\ \implies 1000x = 123.123123\ldots \\\\ \implies 1000x - x = 123.123123\ldots - 0.123123\ldots \\\\ \implies 999x = 123 \\\\ \implies x = (123)/(999)`

It's easy to reverse this method to find the repeating decimal form of
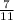`\frac7{11}`. Let

`x = \frac7{11}`

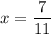
Multiply the numerator and denominator by 9,

`x = (63)/(99)`

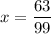
It follows that

`x = (63)/(99) \\\\ \implies 99x = 63 \\\\ 100x - x = 63.6363\ldots - 0.6363\ldots \\\\ \implies x = 0.636363\ldots`

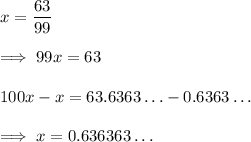
The first 20 digits after the decimal are made up of 10 each of 3 and 6, so the sum is 10 × (3 + 6) = 90.