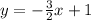Answer:
A. (0, 1) and (2, -2)
B. Slope (m) = -³/2
C. y + 2 = -³/2(x - 2)
D.
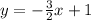
E.

Explanation:
A. Two points on the line from the graph are: (0, 1) and (2, -2)
B. The slope can be calculated using two points, (0, 1) and (2, -2):
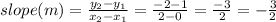
Slope (m) = -³/2
C. Equation in point-slope form is represented as y - b = m(x - a). Where,
(a, b) = any point on the graph.
m = slope.
Substitute (a, b) = (2, -2), and m = -³/2 into the point-slope equation, y - b = m(x - a).
Thus:
y - (-2) = -³/2(x - 2)
y + 2 = -³/2(x - 2)
D. Equation in slope-intercept form, can be written as y = mx + b.
Thus, using the equation in (C), rewrite to get the equation in slope-intercept form.
y + 2 = -³/2(x - 2)
2(y + 2) = -3(x - 2)
2y + 4 = -3x + 6
2y = -3x + 6 - 4
2y = -3x + 2
y = -3x/2 + 2/2
E. Convert the equation in (D) to standard form: