Question

2. The school PTA is sponsoring a dance. They decide to price student tickets at $6.00. It will cost the PTA $250.00 to put on the dance. How many tickets will the PTA need to sell in order to make a profit?​

Answer 1

42 tickets.

Explanation:

To make a profit, the PTA will need to earn at least $251, because it spent $250 on the dance. so we can divide 251/6 = 41 remainder 5, which means we need to sell 42 tickets.

Answer 2

The PTA must sell 42 tickets to make a profit.

Explanation:

To solve this problem, we will have to construct an inequality in which $250 is less than our solution.

Let
`s` = student tickets

Since each student ticket is priced at $6.00, the money raised by the student tickets can be represented by the expression:

`6s`

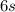
Since it will cost the PTA $250.00 for the dance, the profit will have to be equal to anything greater than $250.00.

Set up your inequality:

`250<6s`

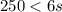
Divide both sides of the inequality by the coefficient of
`s`, which is
`6`:

`41.7=s`

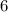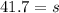
As you can see, we are left with a decimal, but we will have to round to the nearest whole number as the tickets can only be represented as whole numbers:

`42=s`

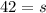
Therefore, the PTA must sell 42 tickets in order to make a profit.

-

You can check your work by substituting the solved value for the tickets into the inequality:

`250<6s`

`250<6(42)`

`250<252`

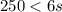
And since $252 is greater than $250 (represents a $2 profit), our solution is correct.