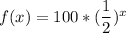Exponential Functions
Exponential functions are typically organized in this format:
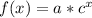
To find the equation given the graph of an exponential function:
- Identify the horizontal asymptote
⇒ asymptote - a line towards which a graph appears to travel but never meets
⇒ If the horizontal asymptote is not equal to 0, we add this at the end of the function equation. - Identify the y-intercept
⇒ This is our a value. - Identify a point on the graph and solve for c
Solving the Question
Identify the horizontal asymptote
In this question, it appears to be x = 0.
Identify the y-intercept
The y-intercept is the value of y at which the graph appears to cross the y-axis. In this graph, it appears to be 100. This is our a value. Plug this into
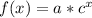 :
:

Solve for c
We can use any point that falls on the graph for this step. For instance, (1,50) appears to be a valid point. Plug this into our equation and solve for c:
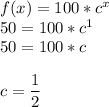
Plug c back into our original equation:
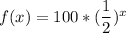
Answer