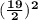Question

If using the method of completing the square to solve the quadratic equation

X2 – 192
3 = 0, which number would have to be added to "complete the
square"?

Help please

Answer 1

The number that would be added to make
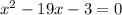`x^2-19x-3=0` a complete square is
`\mathbf{((19)/(2))^2}`

Explanation:

We need to solve the expression
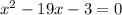`x^2-19x-3=0` using completing the square method.

Completing square method is of form:
`(a-b)^2=a^2-2ab+b^2`

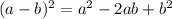
We need to find the term, that it a complete square

The middle term is -19x so, it can be made as: -2(x)(19/2) according to the formula a^2-2ab+b^2

We have a=x and b=19/2

So, adding and subtracting (19/2)^2

`x^2-2(x)((19)/(2) )+((19)/(2))^2- ((19)/(2))^2-3=0\\(x-(19)/(2))^2-(361)/(4)-3=0\\`

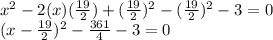
So, the number that would be added to make
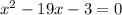`x^2-19x-3=0` a complete square is
`\mathbf{((19)/(2))^2}`