Question

it is any equation in the form f of x = ax to the second power + bx + c where a b and c are real numbers and a not equal to zero . is t a linear equation, quadratic,rational​

Answer 1

The answer to this depends on the accuracy of the way this is transcribed. If the value on the left side of the equals sign is indeed x, then it would be a rational equation. If it is meant to be another scalar value though, then this would be a quadratic equation.

Explanation:

This depends on the what is on the other side of the equals sign. If it is a scalar value, then you are guaranteed a proper quadratic equation. In the example given though:

`x = ax^2 + bx + c`

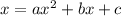
This is not actually true. In this example, we can divide both sides by x, giving us a very different equation:

`x = ax^2 + bx + c\\1 = ax + b + c/x\\ax + c/x = 1b`

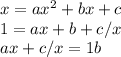
and this equation actually a rational one.