Question

What is the focus of the parabola? y=−1/4x^2 −2x − 2

Answer 1

Explanation:

This is a doozy. You have to know A LOT about parabolas to get to this answer. First and foremost, we will have to complete the square on the x terms and get everything else on the other side of the equals sign with the intention of putting this into standard form which looks like this:

`-4p(y-k)=(x-h)^2`

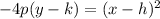
The negative is because the parabola is upside down. We begin breaking it down by multiplying everything by -4 to get:

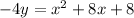`-4y=x^2+8x+8` and subtract that 8 from both sides to get:

`-4y-8=x^2+8x`. Now we'll complete the square on the x terms by taking half the linear term, squaring it, and then adding it to both sides. Our linear term (the number with the x stuck to it) is 8. Half of 8 is 4 ad 4 squared is 16. So we add 16 to both sides to get:

`-4y-8+16=(x^2+8x+16)`

The right side will simplify into a perfect square binomial and the left side we will just combine like terms to get:

`-4y+8=(x+4)^2`

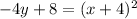
We're getting close. Now we need to just factor out the -4 on the left to get:

`-4(y-2)=(x+4)^2`

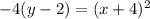
If the standard form is -4p blah blah blah, then p has to be 1. That means that the focus is 1 unit below the vertex. The vertex is (-4, 2). p is the distance between the vertex and the focus. The focus is always on the axis of symmetry. We know that the parabola opens upside down because of the negative sign, and the parabola always wraps itself around the focus. That's why the focus is p units below the vertex. That means that the focus is located at (-4, 1).

Told you it was difficult. I noticed no one helped you with this one and it's been up here for 5 days...