Question

Help me answer this please!!!

Answer 1

39.6 ft.

Explanation:

Height of the top of the goal post would be x + 5.5

So for we need to calculate x first,

For x:

`tan\ \theta = (perpendicular)/(base)\\\\tan\ 61=(x)/(20)\\\\20*tan61=x\\\\x=20*1.732\\\\x=34.64\ ft`

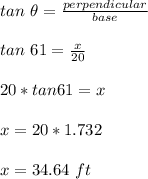
So height of the top of the goal post would be 34.64 + 5.5 which is

39.64 ft. rounding it to nearest tenth would be 39.6ft.

I attached an image too as well check it out.