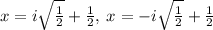Question

Given the quadratic function f(x) = 4x^2 - 4x + 3, determine all possible solutions for f(x) = 0

Answer 1

The solutions to the quadratic function are:

`x=i\sqrt{(1)/(2)}+(1)/(2),\:x=-i\sqrt{(1)/(2)}+(1)/(2)`

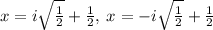
Explanation:

Given the function

`f\left(x\right)\:=\:4x^2\:-\:4x\:+\:3`

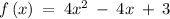
Let us determine all possible solutions for f(x) = 0

`0=4x^2-4x+3`

switch both sides

`4x^2-4x+3=0`

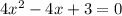
subtract 3 from both sides

`4x^2-4x+3-3=0-3`

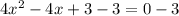
simplify

`4x^2-4x=-3`

Divide both sides by 4

`(4x^2-4x)/(4)=(-3)/(4)`

`x^2-x=-(3)/(4)`

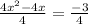
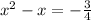
Add (-1/2)² to both sides

`x^2-x+\left(-(1)/(2)\right)^2=-(3)/(4)+\left(-(1)/(2)\right)^2`

`x^2-x+\left(-(1)/(2)\right)^2=-(1)/(2)`

`\left(x-(1)/(2)\right)^2=-(1)/(2)`

`\mathrm{For\:}f^2\left(x\right)=a\mathrm{\:the\:solutions\:are\:}f\left(x\right)=√(a),\:-√(a)`

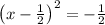
solving

`x-(1)/(2)=\sqrt{-(1)/(2)}`

`x-(1)/(2)=√(-1)\sqrt{(1)/(2)}` ∵
`\sqrt{-(1)/(2)}=√(-1)\sqrt{(1)/(2)}`

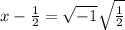as

`√(-1)=i`

so

`x-(1)/(2)=i\sqrt{(1)/(2)}`

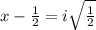
Add 1/2 to both sides

`x-(1)/(2)+(1)/(2)=i\sqrt{(1)/(2)}+(1)/(2)`

`x=i\sqrt{(1)/(2)}+(1)/(2)`

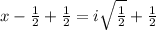
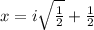
also solving

`x-(1)/(2)=-\sqrt{-(1)/(2)}`

`x-(1)/(2)=-i\sqrt{(1)/(2)}`

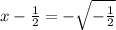
Add 1/2 to both sides

`x-(1)/(2)+(1)/(2)=-i\sqrt{(1)/(2)}+(1)/(2)`

`x=-i\sqrt{(1)/(2)}+(1)/(2)`

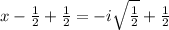
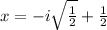
Therefore, the solutions to the quadratic function are:

`x=i\sqrt{(1)/(2)}+(1)/(2),\:x=-i\sqrt{(1)/(2)}+(1)/(2)`