(a) Let
 be the maximum linear speed with which the ball can move in a circle without breaking the cord. Its centripetal/radial acceleration has magnitude
be the maximum linear speed with which the ball can move in a circle without breaking the cord. Its centripetal/radial acceleration has magnitude

where
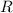 is the radius of the circle.
is the radius of the circle.
The tension in the cord is what makes the ball move in its plane. By Newton's second law, the maximum net force on it is
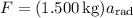
so that
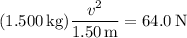
Solve for
 :
:
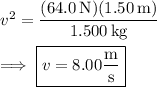
(b) The net force equation in part (a) leads us to the relation

so that
 is directly proportional to the square root of
is directly proportional to the square root of
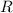 . As the radius
. As the radius
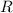 increases, the maximum linear speed
increases, the maximum linear speed
 will also increase, so the cord is less likely to break if we keep up the same speed.
will also increase, so the cord is less likely to break if we keep up the same speed.