Question

Writing equation of the line that passes through the given points (2, 3); (0,-1)

Answer 1

`y = 2x - 1`

You should also try solving it yourself to make sure I did not make any mistake.

Explanation:

Equation:

`y = mx + b`

first we need the slope

`slope = (y1 - y2)/(x1 - x2)`

`slope = (3 - ( - 1))/(2 - 0) = (4)/(2) = 2`

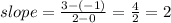
So far the equation will look like this

`y = 2x + b`

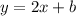
Now to get b just pick one point and insert it into the equation. So I'll just pick (2,3)

`3 = 2 * 2 + b`

when you solve this equation you'll get b

`b = - 1`

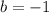
We could also check if we get the same answer if we instead use point (0,-1)

`- 1 = 2 * 0 + b`

`b = - 1`

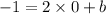
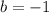
Now we have the equation!

`y = 2x - 1`