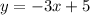Question

What is an equation of the line that passes through the points (1,2) and (2,-1) 

Answer 1

`y = - 3x + 5`

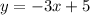
You should also try solving it yourself to make sure I did not make any mistake.

Explanation:

Equation

`y = mx + b`

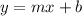
First we need to know the slope

`slope = (y1 - y2)/(x1 - x2)`

`slope = (2 - ( - 1))/(1 - 2) = (3)/( - 1) = - 3`

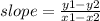
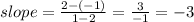
So far the equation will look like this

`y = - 3x + b`

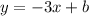
To get the b you insert a point into the equation like this. I picked point (1,2)

`2 = - 3 * 1 + b`

`b = 5`

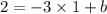
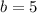
We could also check it with the other point and see if we get the same answer.

`- 1 = - 3 * 2 + b`

`b = 5`

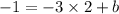
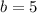
So the equation is

`y = - 3x + 5`