Assuming
 is a non-negative real number...
is a non-negative real number...
Raise both sides to the power 2 :
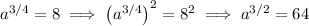
which follows from the exponent product property,
 . In particular, 3/4 × 2 = 6/4 = 3/2.
. In particular, 3/4 × 2 = 6/4 = 3/2.
Raise both sides to the power 1/3 :
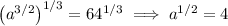
where we use the same property as before, and 4³ = 64. This time, 3/2 × 1/3 = 3/6 = 1/2.
Take the reciprocal of both sides. This negates the exponent, so we end up with
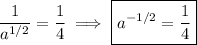
Of course, you could also solve for
 immediately by raising both sides of the original equation to the power 4/3. We have 4/3 × 3/4 = 12/12 = 1, so
immediately by raising both sides of the original equation to the power 4/3. We have 4/3 × 3/4 = 12/12 = 1, so
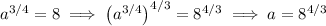
Now 2³ = 8, so
 , and since 4² = 16, it follows that
, and since 4² = 16, it follows that
