
____________________________________
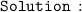
[ let the point at which line segments SV and RT intersects be O ]
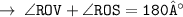
[ linear pair ]
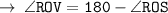
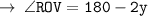
____________________________________
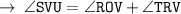
[ Exterior angle = sum of opposite interior angles ]
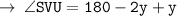
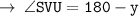
( let it be equation 1 )
____________________________________
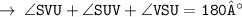
[ Sum of angles of Triangle ]
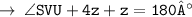
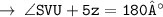
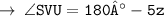
( let it be equation 2 )
____________________________________
By comparing both equations :
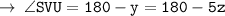
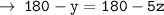
( Add 180° on both sides )
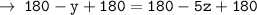
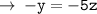
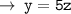
Answered by : ❝ AǫᴜᴀWɪᴢ ❞