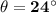Question

4. A hot air balloon hovers 100 feet about the ground. The balloon is tethered to the ground with a

rope that is 250 feet long. At what angle of elevation, is the rope attached to the ground? Round
you answer to the nearest degree.

Answer 1

`\theta=24^\circ`

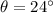
Explanation:

Trigonometry and Right Triangles:

The ratios of the sides of a right triangle are called trigonometric ratios. Any angle or side length can be calculated using the appropriate trigonometric ratio.

Please refer to the image below. The balloon is 100 feet high and the rope has a length of 250 feet. The right triangle formed allows us to apply a trigonometric ratio that relates the two given side lengths: the hypotenuse and the opposite leg to angle θ.

The sine ratio is defined as:

`\displaystyle \sin\theta=\frac{\text{opposite leg}}{\text{hypotenuse}}`

`\displaystyle \sin\theta=(100)/(250)=0.4`

`\displaystyle \sin\theta=0.4`

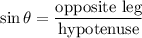
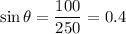
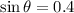
Calculating θ:

`\theta=\arcsin 0.4`

`\theta=23.6^\circ`

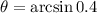
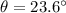
To the nearest degree:

`\mathbf{\theta=24^\circ}`