Answer:
From the graph, it is clear that the point of intersection is:
And the x-coordinate of the point of intersection for the two lines is:
Explanation:
- As we know that the solution of the system of equations is the point of intersection. Let us solve it.
Given the system of equations
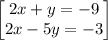
solving the system of equations
subtracting 2x+y = -9 from 2x-5y = -3




so
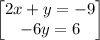
solving for y

Divide both sides by -6

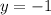
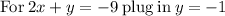

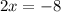
Divide both sides by 2
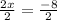
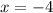
Thus, the x-coordinate of the point of intersection for the two lines below will be:
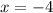
Also, the graph is attached.
From the graph, it is clear that the point of intersection is:
And the x-coordinate of the point of intersection for the two lines is: