Question

Albert needs $133 to buy a new hard drive. He earns $4.75 for each car he washes. If he spends $19 in supplies, write and solve an equation to find the number of cars he needs to wash to reach his goal.

Answer 1

Albert needs 32 cars to wash to reach his goal.

Explanation:

We know that the slope-intercept form of a linear function is

`y = mx+b`

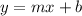
where m is the slope or rate of change and b is the y-intercept

It is stated that Albert needs $133 to buy a new hard drive.

• Let 'y' be the amount Albert needs.

As earns $4.75 for each car he washes. Thus, $4.75 the rate of change or slope will be.

As he spends $19 on supplies. Since it is an expense, so -19 is basically the y-intercept 'b'.

Let 'x' be the number of cars he needs to wash to reach his goal.

Thus, substituting the value m = 4.75, y = 133, and b=-19 in the slope-intercept form of a linear function

y = mx+b

133 = 4.75x - 19

133+19 = 4.75x

152 = 4.75x

x = 152 / 4.75

x = 32

Therefore, Albert needs 32 cars to wash to reach his goal.