Answer:
The speed of jet in still air is 750 miles per hour and speed of wind is 130 miles per hour.
Explanation:
Given that:
Distance traveled by jet against the wind = 2480 miles in 4 hours
Combined speed =
 =
=
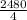
Combined speed = 620 miles per hour
Distance traveled with wind = 7040 miles in 8 hours
Combined speed =
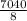
Combined speed = 880
Let,
Speed of jet = x
Speed of wind = y
When jet travels against the wind, the speed will be subtracted
x-y=620 Eqn 1
When jet travels with the wind, the speed will be added
x+y=880 Eqn 2
Adding Eqn 1 and 2
(x-y)+(x+y)=620+880
x-y+x+y=1500
2x=1500
Dividing both sides by 2
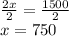
Putting x=750 in Eqn 2
750+y=880
y=880-750
y=130
Hence,
The speed of jet in still air is 750 miles per hour and speed of wind is 130 miles per hour.