Question

Determine whether the table of values below represents a linear function. If it represents a linear function, write the function. If it does not represent a linear function, explain why not.

Answer 1

The equation of a linear function is:

• 
  `y = 2x+4`

Explanation:

Given the table

x y

-10 -16

-3 -2

1 6

2 8

Determining the slope between the points (-10, -16), (-3, -2)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-10,\:-16\right),\:\left(x_2,\:y_2\right)=\left(-3,\:-2\right)`

`m=(-2-\left(-16\right))/(-3-\left(-10\right))`

`m=2`

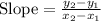
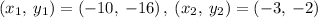
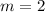
Determining the slope between the points (-3, -2), (1, 6)

`m=(6-\left(-2\right))/(1-\left(-3\right))`

`m=2`

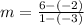
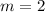
Determining the slope between the points (1, 6),(2, 8)

`m=(8-6)/(2-1)`

`m = 2`

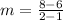
As the slope between the points is the same. Thus, the table represents the linear function.

Using the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

substituting the values m = 2 and any point let say (1, 6)

`y - 6 = 2(x-1)`

`y-6 = 2x-2`

`y = 2x-2+6`

`y = 2x+4`

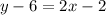
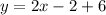
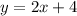
Therefore, the equation of a linear function is:

• 
  `y = 2x+4`