Question

A line has a slope of 6 and includes the points (n,1) and (8,5). What is the value of n?

Answer 1

The value of n:

• 
  `n=(22)/(3)`

Explanation:

Given that the line has slope 6.

i.e. m = 6

The line includes the points

• (n, 1)

• (8, 5)

Using the formula to find the slope of the points

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(n,\:1\right),\:\left(x_2,\:y_2\right)=\left(8,\:5\right)`

`m=(4)/(8-n)`

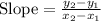
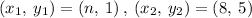
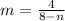
as

m = 6

substituting m = 6

`6=(4)/(8-n)`

`6\left(8-n\right)=4`

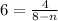
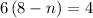
Divide both sides by 6

`(6\left(8-n\right))/(6)=(4)/(6)`

`8-n=(2)/(3)`

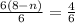
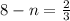
subtract 8 from both sides

`8-n-8=(2)/(3)-8`

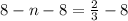
simplify

`-n=-(22)/(3)`

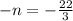
Divide both sides by -1

`(-n)/(-1)=(-(22)/(3))/(-1)`

`n=(22)/(3)`

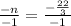
Therefore, the value of n:

• 
  `n=(22)/(3)`