Question

Part A

Based on the graph, how many zeros does the polynomial function, f(x) = -x^4 - 3x^3 + 6x^2 + 8x have?


Part B

What are the zeroes of the above polynomial function?

A. -4,0,2,3
B. 0, 2 only
C. -4,-1, 0, 2
D. -4, 2 only

Answer 1

Part A: There are 4 zeros of the polynomial function f(x)

Part B: The zeroes of the polynomial function f(x) are -4, -1, 0, 2 ⇒ C

Explanation:

The zeroes of a function are the x-coordinates of the point of intersection between the graph of the function and the x-axis (x-intercepts) which means values of x at y = 0

Part A:

In the given graph

∵ The graph of the function f(x) = -
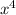`x^(4)` - 3x³ + 6x² + 8x intersects the x-axis

at 4 points

→ That means there are 4 values of x have y = 0

∴ The number of zeroes of the function is 4

∴ There are 4 zeros of the polynomial function f(x)

Part B:

∵ The graph intersects the x-axis at points (-4, 0), (-1, 0), (0, 0), (2, 0)

→ That means the values of x at y = 0 are -4, -1, 0, 2

∴ f(x) = 0 at x = -4, -1, 0, 2

∴ The zeroes of the polynomial function f(x) are -4, -1, 0, 2