Answer:
12 seconds
Step-by-step explanation:
Time taken by 50cm³ of oxygen to diffuse from pinhole
= 1 minute = 60 seconds
⠀
⠀
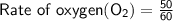
⠀
⠀
⠀
Let time taken by 50cm³ of hydrogen to diffuse from pinhole = t seconds
⠀
⠀
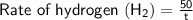
⠀
⠀
⠀
According to the formula
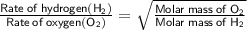
⠀
⠀
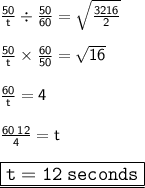
⠀
⠀
⠀
Henceforth, the time taken by 50cm³ of hydrogen to diffuse is 12 seconds.
⠀
⠀
Thank you!