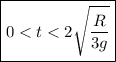Disclaimer: I ended up finding what's asked for in the reverse order (e)-(a).
At time
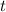 , the horizontal position
, the horizontal position
 and vertical position
and vertical position
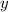 of the ball are given respectively by
of the ball are given respectively by
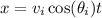
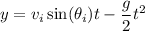
and the horizontal velocity
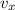 and vertical velocity
and vertical velocity
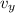 are
are
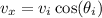
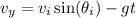
The ball reaches its maximum height with
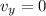 . At this point, the ball has zero vertical velocity. This happens when
. At this point, the ball has zero vertical velocity. This happens when
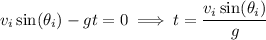
which means
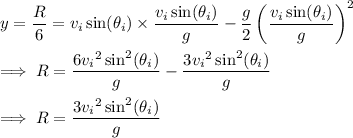
At the same time, the ball will have traveled half its horizontal range, so
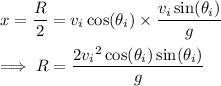
Solve for
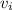 and
and
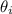 :
:
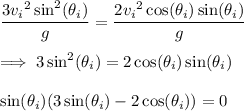
Since
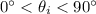 , we cannot have
, we cannot have
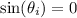 , so we're left with (e)
, so we're left with (e)
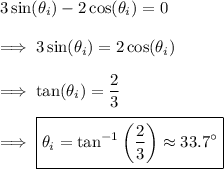
Now,
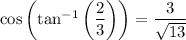
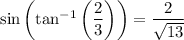
so it follows that (d)

Knowing the initial speed and angle, the initial vertical component of velocity is (c)
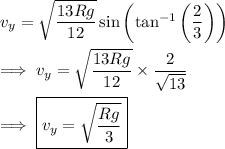
We mentioned earlier that the vertical velocity is zero at maximum height, so the speed of the ball is entirely determined by the horizontal component. (b)
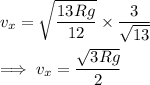
Then with
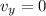 , the ball's speed
, the ball's speed
 is
is

Finally, in the work leading up to part (e), we showed the time to maximum height is
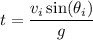
but this is just half the total time the ball spends in the air. The total airtime is then
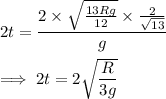
and the ball is in the air over the interval (a)