Part A
The notation
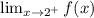 means that we're approaching x = 2 from the right hand side (aka positive side). This is known as a right hand limit.
means that we're approaching x = 2 from the right hand side (aka positive side). This is known as a right hand limit.
So we could start at say x = 2.5 and get closer to 2 by getting to x = 2.4 then to x = 2.3 then 2.2, 2.1, 2.01, 2.001, etc
We don't actually arrive at x = 2 itself. We simply move closer and closer.
Since we're on the positive or right hand side of 2, this means we go with the rule involving x > 2
Therefore f(x) = (x/2) + 1
Plug in x = 2 to find that...
f(x) = (x/2) + 1
f(2) = (2/2) + 1
f(2) = 2
This shows
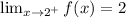
Then for the left hand limit
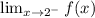 , we'll involve x < 2 and we go for the first piece. So,
, we'll involve x < 2 and we go for the first piece. So,
f(x) = 3-x
f(2) = 3-2
f(2) = 1
Therefore,
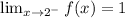
===============================================================
Part B
Because
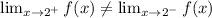 this means that the limit
this means that the limit
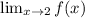 does not exist.
does not exist.
If you are a visual learner, check out the graph below of the piecewise function. Notice the gap or disconnect at x = 2. This can be thought of as two roads that are disconnected. There's no way for a car to go from one road to the other. Because of this disconnect, the limit doesn't exist at x = 2.
===============================================================
Part C
You'll follow the same type of steps shown in part A.
However, keep in mind that x = 4 is above x = 2, so we'll deal with x > 2 only.
So you'd only involve the second piece f(x) = (x/2) + 1
You should find that f(4) = 3, and that both left and right hand limits equal this value. The left and right hand limits approach the same y value. The limit does exist here. There are no gaps to worry about when x = 4.
===============================================================
Part D
As mentioned earlier, since
 , this means the limit
, this means the limit
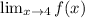 does exist and it's equal to 3.
does exist and it's equal to 3.
As x gets closer and closer to 4, the y values are approaching 3. This applies to both directions.