Question

Need help figuring out the answers

Answer 1

3, -1, 1 and 0

Explanation:

An expression is undefined when the denominator is equal to 0 as you cannot divide by 0 in Mathematics. Therefore you are looking for the values of x which will result in either or both denominators equaling 0.

This simply means finding the solutions to the quadratics in the denominators.

First equation is
`x^(2) -2x-3`.

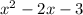One way you can solve this equation is using factorization (putting the equation into two sets of brackets which show the solutions) which puts the equation in the solvable form: (ax+b)(cx+d).

Firstly, we can deduct that a and c are both 1 as ax and cx multiply to give the x^2 term, the co-efficient of which is 1. Since only 1 and 1 can multiply to 1, a and c must both be 1.

Now, in order to work out b and d we need to find the possible factor combinations for -3 as b and d multiply to give the constant term. The only possible combination is 1x3, therefore b and d can either be -1 and 3, or -3 and 1.

To work this out we look at the x term. We see it is -2x. b and d will add to give the co-efficient.

Therefore we know that they are -3 and 1 as -3+1 = -2

We now have the equation: (x+1)(x-3)

Setting it to 0 gives us:
`(x+1)(x-3)=0`

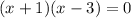
This tells us the solutions to this equation are x= -1 and x= 3 as substituting these values for x will result in a bracket adding to 0 so both those options can be selected as your answer.

The second equation
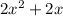`2x^(2) +2x` can be approached with a slightly easier method. Both terms have a 2x, so we can condense it into a bracket by dividing both terms by the common factor and moving the factor outside. Factorizing this equation in this fashion gives us:
`2x(x+1)=0`

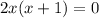
Now our solutions are x=0 and x=1.

Combined from both equations the correct options are: 3, -1, 1 and 0.

Hope this helped!